Question

A parabola with vertex (1,5) and y-intercept

(0,2) crosses the x-axis in two places. One x-
intercept is at (-0.29,0). Find the other x-
intercept. Separate the values with a comma.

Answer 1

So the other x-intercept we are looking for is (2.29 , 0).

Explanation:

The equation for a parabola in vertex form is

`y=a(x-h)^2+k` where (h,k) is the vertex.

So we are given (h,k)=(1,5) so let's plug that in. This gives us the following equation for our parabola:

`y=a(x-1)^2+5`.

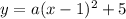Now we need to find
`a`. Let's find
`a` by using another point (x,y) given. We are given that (0,2) is on our parabola. So when x is 0, y is 2.

This gives us the equation:

`2=a(0-1)^2+5`

`2=a(-1)^2+5`

`2=a(1)+5`

`2=a+5`

`2-5=a`

`-3=a`

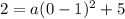
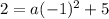
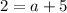
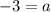
So our parabola in vertex form looks like this:

`y=-3(x-1)^2+5`

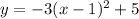
Now we are asked to find the x-intercepts.

You can find the x-intercepts by setting y equal to 0 and solving for x.

So let's do that:

`0=-3(x-1)^2+5`

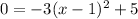
Subtract 5 on both sides:

`-5=-3(x-1)^2`

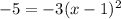
Divide both sides by -3:

`(5)/(3)=(x-1)^2`

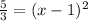
Take the square root of both sides:

`\pm \sqrt{(5)/(3)}=x-1`

Add 1 on both sides:

`\pm \sqrt{(5)/(3)}+1=x`

So the two solutions in exact form are

`x=\sqrt{(5)/(3)}+1 \text{ or } -\sqrt{(5)/(3)}+1`

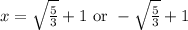
Putting both into calculator (separately) gives:

`x \approx 2.29 \text{ or } -0.29`

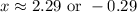
So the other x-intercept we are looking for is (2.29 , 0).