Question

A person standing close to the edge on top of a 24-foot building throws a ball vertically upward. The quadratic function h(t)=−16t^2+92t+24 models the ball's height about the ground, h(t), in feet, t seconds after it was thrown.

a) What is the maximum height of the ball?

__feet

b) How many seconds does it take until the ball hits the ground?

____ seconds

Answer 1

The maximum height of the ball is calculated to be at 2.875 seconds, and by inserting this time back into the height function, we get the max height. To determine when the ball hits the ground, we solve the quadratic function for when h(t) equals zero, finding that it occurs at approximately 5.4 seconds post launch.

Step-by-step explanation:

To calculate the maximum height of the ball, we need to find the vertex of the quadratic function, which gives us the time when the maximum height is reached. The function is in the form h(t) = -16t^2 + 92t + 24. The time at which the maximum height occurs can be found using the formula -b/(2a), where a and b are coefficients from the quadratic function. Here, a = -16 and b = 92, so the time is t = -92/(2*(-16)) = 92/32 = 2.875 seconds. Inserting this back into the height function gives us the maximum height:

h(2.875) = -16(2.875)^2 + 92(2.875) + 24

Now, to find when the ball hits the ground, we need to find the positive root of the height function where h(t) = 0. The quadratic formula h(t) = -16t^2 + 92t + 24 is used to find the time values when the ball is at the ground level. Solving this equation, we get two possible times, and we're interested in the positive one since time cannot be negative.

Thus, we get that the ball reaches the ground at approximately 5.4 seconds.

Answer 2

a) maximum height is 156.25 ft

b) 6 seconds

Step-by-step explanation:

a) The maximum height can be found by finding the y-coordinate of the vertex. The vertex is the highest point in a parabola opened downward.

I start with by finding the t-coordinate of the vertex.

The t-coordinate of the vertex is
`(-b)/(2a)` where the expression
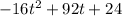`-16t^2+92t+24` will need to be compared to
`at^2+bt+c`.

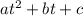We see that
`a=-16,b=92,c=24`.

So the t-coordinate of the vertex is
`(-b)/(2a)=(-92)/(2(-16))=(-92)/(-32)=(23)/(8)`.

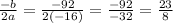We can find the h, the height, that corresponds to this t by using the equation
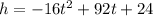`h=-16t^2+92t+24` where
`t=(23)/(8)`.

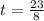So inserting 23/8 for
`t`.

`-16(23/8)^2+92(23/8)+24`

Plugging into calculator gives you 625/4.

So the maximum height is 625/4 or 156.25.

b) Let's find how long it takes the ball to hit the ground. If the ball is on the ground, then the distance between the ball and the ground is 0. So we are looking to solve h(t)=0 for t.

So this is equation we are solving for t:

`-16t^2+92t+24=0`

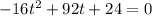
These numbers are big but since all the terms have a common factor we can make them slightly smaller.

That is, we are going to divide both sides by -4 and see

`4t^2-23t-6=0`

It looks like it could be possible to factor.

a=4

b=-23

c=-6

We need to find two numbers that multiply to be ac and add up to be b.

a*c=4(-6)=-24

b=-23

So -24=-24*1 and -23=-24+1.

We are going to replace -23t with -24t+1t giving up something that should be factorable by grouping.

`4t^2-23t-6=0`

`4t^2-24t+1t-6=0`

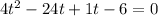
Group the first 2 together and group the last two together:

`(4t^2-24t)+(1t-6)=0`

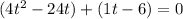
Factor what you can from each pair:

`4t(t-6)+1(t-6)=0`

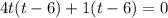
Now each term has a common factor of (t-6) so factor that out giving you:

`(t-6)(4t+1)=0`

Set both factors equal to 0 giving you

t-6=0 or 4t+1=0

t=6 or 4t =-1

t=6 or t=-1/4

So it hit the ground in 6 seconds.