Question

Peter works part time for 3 hours every day and Cindy works part time for 2 hours every day.

a. If both of them get $4.50 an hour, write an inequality to compare Peter’s and Cindy’s earnings.
b. What should Cindy’s per-hour income be so that she earns at least $14 a day? Write an inequality and an explanation of
how to solve it.

Answer 1

Peter works part time for 3 hours every day and Cindy works part time for 2 hours every day.

Part A:

Peter's earning in 3 hours is =
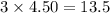`3*4.50=13.5` dollars

Cindy's earnings in 2 hours is =
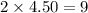`2*4.50=9` dollars

We can define the inequality as:
`9<13.50`

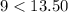
Part B:

Let Cindy's earnings be C and number of hours needed be H.

We have to find her per hour income so that C ≥ 14

As Cindy works 2 hours per day, the inequality becomes 2H ≥ 14

So, we have
`H\geq 7`

This means Cindy's per hour income should be at least $7 per hour so that she earns $14 a day.

Answer 2

a. We can say that P > C, where 'P' represents Peter's earnings and 'C' represents Cindy's earnings.

Given that P = 3h and C = 2h, where h =$4.50. We can say also that 3h > 2h.

b. If Cindy wants to earn at least $14 a day working two hours. Then:

2h ≥ $14

To solve the problem, we just need to solve for 'h':

h ≥ $7

Therefore, se should earn more or equal to $14 per hour.