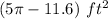Question

What is the shaded portion of the circle

Answer 1

`(5\pi-11.6)\ ft^(2)`

Explanation:

we know that

The area of the shaded region is equal to the area of the sector minus the area of the triangle

step 1

Find the area of the circle

the area of the circle is equal to

`A=\pi r^(2)`

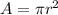
we have

`r=5\ ft`

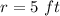
substitute

`A=\pi (5)^(2)`

`A=25\pi\ ft^(2)`

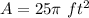
step 2

Find the area of the sector

we know that

The area of the circle subtends a central angle of 360 degrees

so

by proportion find out the area of a sector by a central angle of 72 degrees

`(25\pi)/(360)=(x)/(72)\\ \\x=72*25\pi /360\\ \\x=5\pi\ ft^(2)`

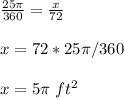
step 3

Find the area of triangle

The area of the triangle is equal to

`A=(1)/(2)(2.9+2.9)(4)= 11.6\ ft^(2)`

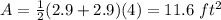
step 4

Find the area of the shaded region

Subtract the area of the triangle from the area of the sector

`(5\pi-11.6)\ ft^(2)`