Question

Y = −(x + 4)2 − 7 vertex

Answer 1

The vertex (h,k) is (-4,-7).

Explanation:

I assume you are looking for the vertex
`y=-4(x+4)^2-7`.

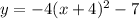The vertex form of a quadratic is
`y=a(x-h)^2+k` where the vertex is (h,k) and a tells us if the parabola is open down (if a<0) or up (if a>0). a also tells us if it is stretched or compressed.

Anyways if you compare
`y=-4(x+4)^2-7` to
`y=a(x-h)^2+k` , you should see that
`a=-4,h=-4,k=-7`.

So the vertex (h,k) is (-4,-7).

Answer 2

The vertex is
`(-4,-7)`

Explanation:

The vertex form of a parabola is given by:

`y=a(x-h)^2+k`, where (h,k) is the vertex and
`a` is the leading coefficient.

The given parabola has equation:

`y=-1(x+4)^2-7`

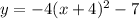When we compare to the vertex form, we have

`-h=4\implies h=-4` and
`k=-7`.

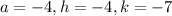Therefore the vertex is (-4,-7)