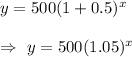Question

The value of a collector’s item is expected to increase exponentially each year. The item is purchased for $500. After 2 years, the item is worth $551.25. Which equation represents y, the value of the item after x years?y = 500(0.05)xy = 500(1.05)xy = 500(0.1025)xy = 500(1.1025)x

Answer 1

y = 500(1.05)^x.

Explanation:

551.25 = 500x^2 where x is the multiplier for each year.

x^2 = 551.25/500

x = 1.05

So the value after x years is 500(1.05)^x.

Answer 2

Answer:
`y=500(1.05)^x`

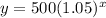
Explanation:

The exponential growth equation is given by :-

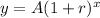`y=A(1+r)^x` (1)

, where A is the initial value of , r is the rate of growth ( in decimal) and t is the time period ( in years).

Given : The value of a collector’s item is expected to increase exponentially each year.

The item is purchased for $500. After 2 years, the item is worth $551.25.

Put A= 500 ; t= 2 and y= 551.25 in (1), we get

`551.25=500(1+r)^2\\\\\Rightarrow\ (1+r)^2=(551.25)/(500)\\\\\Rightarrow (1+r)^2=1.1025`

Taking square root on both sides , we get

`1+r=√(1.1025)=1.05\\\\\Rightarrow\ r=1.05-1=0.5`

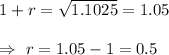
Now, put A= 500 and r= 0.5 in (1), we get the equation represents y, the value of the item after x years as :

`y=500(1+0.5)^x\\\\\Rightarrow\ y=500(1.05)^x`