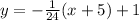Answer:
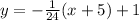
Explanation
The directrix y=7, is above the y-value of the focus. The parabola must will open downwards.
Such parabola has equation of the form,
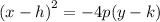
where (h,k) is the vertex.
The vertex is the midway from the focus to the directrix
The x-value of the vertex is x=-5 because it is on a vertical line that goes through (-5,-5).
The y-value of the vertex is
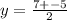
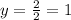
The equation of the parabola now becomes

p is the distance from the focus to the vertex which is p=|7-1|=6
Substitute the value of p to get:
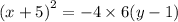
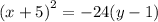
We solve for y to get: