Answer:
A rectangular prism in which BA = 20 and h = 6 has a volume of 120 units3; therefore, Shannon is correct
Explanation:
step 1
Find the area of the base of the rectangular pyramid
we know that
The volume of the rectangular pyramid is equal to

where
B is the area of the base
H is the height of the pyramid
we have
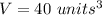
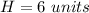
substitute and solve for B
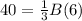
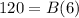
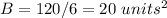
step 2
Find the volume of the rectangular prism with the same base area and height
we know that
The volume of the rectangular prism is equal to

we have
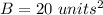
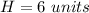
substitute
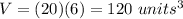
therefore
The rectangular prism has a volume that is three times the size of the given rectangular pyramid. Shannon is correct