Answer:
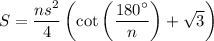
Explanation:
A "regular pyramid" is a pyramid whose base is a regular polygon and whose edges are all the same length. Thus each face is an equilateral triangle.
A hexagonal regular pyramid will look like a hexagonal pancake, as the vertical height of it will be zero. A regular pyramid with 7 or more faces cannot exist, because the apexes of the triangular faces cannot meet at a point.
__
For an edge length of "s", the area of each triangular face is (√3)/4×s². There are n of those faces, so the lateral area (LA) will be ...
LA = ns²(√3)/4
The area of the regular polygon base will be the product of half its perimeter and the length of its apothem (a). The apothem is ...
a = (s/2)cot(180°/n)
So, the area of the base (BA) is ...
BA = (1/2)(ns)(s/2)cot(180°/n) = ns²cot(180°/n)/4
The total surface area of the regular pyramid is then ...
S = BA + LA
S = (ns²/4)(cot(180°/n) +√3) . . . . for edge length s and n faces (3≤n≤5)