Answer:
11
Explanation:
Ok so we aren't looking to maximize profits which is equivalent to finding the vertex of the parabola.
But we want to know what is the highest number of x so that our we aren't losing money. We aren't losing money when our profit is 0.
So we are asked to solve P(x)=0 for x and take the highest x of that equation.
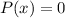
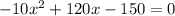
I'm going to divide both sides by -10 to make the numbers easier to work with later.
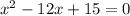
I'm going to use the quadratic formula.
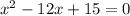 when compared to
when compared to
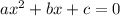 gives us
gives us
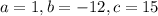 .
.
We are going to plug this into our quadratic formula:
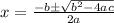 .
.
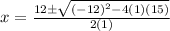
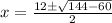
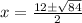
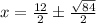
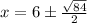
I'm ready to put this into my calculator.
The one with the plus gives me 10.5826 approximately.
The one with the minus gives me 1.4174 approximately.
The 10.5826 is the higher number.
So about 11 dollars.