Question

Use the functions to answer the question.

f(x)=x^2+13 g(x)=12x−14

At what values of x do the functions intersect?

Select all that apply.

9
3
−3
−9

Answer 1

x = 9 and x = 3

Explanation:

Given

f(x) = x² + 13 and g(x) = 12x - 14

To find the points of intersection equate the 2 functions, that is

f(x) = g(x)

x² + 13 = 12x - 14 ← subtract 12x - 14 from both sides

x² - 12x + 27 = 0 ← in standard form

Consider the factors of the constant term ( + 27) which sum to give the coefficient of the x- term ( - 12)

The factors are - 3 and - 9, since

- 3 × - 9 = + 27 and - 3 - 9 = - 12, hence

(x - 3)(x - 9) = 0

Equate each factor to zero and solve for x

x - 3 = 0 ⇒ x = 3

x - 9 = 0 ⇒ x = 9

The functions intersect at x = 3 and x = 9

Answer 2

3 and 9

if f(x)=x^2+13 and g(x)=12x-14

Explanation:

So when we are looking for the intersection of two functions, we are trying to figure out when they are the same. When you think same, you should think equal (=).

So we want to find when f(x)=g(x) for x.

f(x)=g(x)

`x^2+13=12x-14`

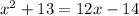
Let's get everything to one side.

Subtracting 12x and adding 14 to both sides.

`x^2+13+14-12x=0`

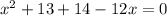
I'm going to reorder the left hand side and also simplify the 13+14 part:

`x^2-12x+27=0`

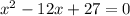
Now since the coefficent of x^2 is just 1 our job is to find two numbers that multiply to be 27 and add up to be -12.

Those numbers are -3 and -9 since -3(-9)=27 and -3+(-9)=-12.

So the factored form of our equation is

`(x-3)(x-9)=0`

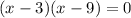
Since the product is 0, then at least one of the factors must be 0.

So we want to solve both x-3=0 and x-9=0.

x-3=0 can be solved by adding 3 on both sides. This gives us x=3.

x-9=9 can be solved by adding 9 on both sides. This gives us x=9.

The intersection of f and g happens at x=3 or x=9.