Answer:
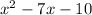 is consider prime (also known as not factorable over the rationals)
is consider prime (also known as not factorable over the rationals)
Explanation:
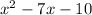 is consider prime.
is consider prime.
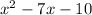 comparing to
comparing to
 gives you
gives you
 .
.
Since a=1, all you have to do is find two numbers that multiply to be -10 and add up to be -7.
Here are all the integer pairs that multiply to be -10:
-1(10)
1(-10)
2(-5)
-2(5)
Now you will see none of those pairs adds to be -7:
-1+10=9
1+(-10)=-9
2+(-5)=-3
-2+5=3
So this is not factorable over the real numbers.
Now if you had something like
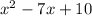 , that would be a different story. You can find two numbers that multiply to be 10 and add up to be -7. Those numbers are -2 and -5 since -2(-5)=10 and -2+(-5)=-7. So the factored form of
, that would be a different story. You can find two numbers that multiply to be 10 and add up to be -7. Those numbers are -2 and -5 since -2(-5)=10 and -2+(-5)=-7. So the factored form of
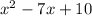 is
is
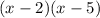 .
.