Answer:
Dotted linear inequality shaded above passes through (0, 4) and (4, 0). Solid exponential inequality shaded below passes through (negative 2,2) & (0,5)
Explanation:
we have
 ----> inequality A
----> inequality A
The solution of the inequality A is the shaded area above the dotted line
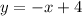
The dotted line passes through the points (0,4) and (4,0) (y and x-intercepts)
and
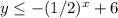 -----> inequality B
-----> inequality B
The solution of the inequality B is the shaded area above the solid line

The solid line passes through the points (0,5) and (-2,2)
therefore
The solution of the system of inequalities is the shaded area between the dotted line and the solid line
see the attached figure
Dotted linear inequality shaded above passes through (0, 4) and (4, 0). Solid exponential inequality shaded below passes through (negative 2,2) & (0,5)