Question

Examine the following system of inequalities.

{y <−1/4x+4 and y>(x+4)^2
Which option shows the graph of the system?

Dotted linear inequality shaded above passes through (0, 4) & (4,5). Dotted parabolic inequality shaded below passes through (negative 6,4), (negative 4, 0) & (negative 2, 4).

Dotted linear inequality shaded below passes through (0, 4) & (4,3). Dotted parabolic inequality shaded above passes through points (negative 6,4), (negative 4, 0) & (negative 2, 4).

Dotted linear inequality shaded below passes through (0, 4) & (4,5). Dotted parabolic inequality shaded above passes through points (negative 6,4), (negative 4, 0) & (negative 2, 4).

Dotted linear inequality shaded above passes through (0, 4) & (4,3). Dotted parabolic inequality shaded below passes through (negative 6,4), (negative 4, 0) & (negative 2, 4).

Answer 1

Dotted linear inequality shaded below passes through (0, 4) & (4,3). Dotted parabolic inequality shaded above passes through points (negative 6,4), (negative 4, 0) & (negative 2, 4).

Explanation:

Hello! Let me help you to find the correct option to this problem. First of all, we have the following system of inequalities:

`\left\{ \begin{array}{c}y< -(1)/(4)x+4\\y>(x+4)^(2)\end{array}\right.`

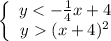
To solve this, let's write the following equations:

FIRST:

`y=-(1)/(4)x+4`

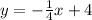
This is a linear function written in slope-intercept form as
`y=mx+b`. So, the slope
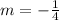`m=-(1)/(4)` and the y-intercept is
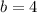`b=4`. Since in the inequality we have the symbol < then the graph of the line must be dotted. To get the shaded region, let's take a point, say,
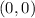`(0, 0)` and let's test whether the region is above or below the graph. So:

`y< -(1)/(4)x+4 \\ \\ Let \ x=y=0 \\ \\ 0<-(1)/(4)(0)+4 \\ \\ 0<4 \ True!`

Since the expression is true, then the region is the one including point
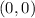`(0, 0)`, that is, it's shaded below.

SECOND:

`y=(x+4)^(2)`

This is a parabola that opens upward and whose vertex is
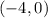`(-4,0)`. Since in the inequality we have the symbol > then the graph of the parabola must be dotted. Let's take the same point
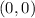`(0, 0)` to test whether the region is above or below the graph. So:

`y>(x+4)^(2) \\ \\ Let \ x=y=0 \\ \\ 0>(0+4)^2\\ \\ 0>16 \ False!`

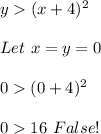
Since the expression is false, then the region is the one that doesn't include point
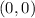`(0, 0)`, that is, it's shaded above

____________________

On the other hand, testing points (0, 4) and (4,3) on the linear function:

`y=-(1)/(4)x+4 \\ \\ \\ \bullet \ (0,4): \\ \\ y=-(1)/(4)(0)+4 \therefore y=4 \\ \\ \\ \bullet \ (4,3): \\ \\ y=-(1)/(4)(4)+4 \therefore y=3`

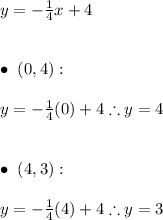
So the line passes through these two points.

Now, testing points (negative 6,4), (negative 4, 0) & (negative 2, 4) on the parabola:

`y=(x+4)^2 \\ \\ \\ \bullet \ (-6,4): \\ \\ y=(-6+4)^2 \therefore y=(-2)^2 \therefore y=4 \\ \\ \\ \bullet \ (-4,0): \\ \\ y=(-4+4)^2 \therefore y=0 \\ \\ \\ \bullet \ (-2,4): \\ \\ y=(-2+4)^2 \therefore y=(2)^2 \therefore y=4`

So the line passes through these three points.

Finally, the shaded region is shown below.