Question

Sin x + cos x = cos x/1-tanx + sin x/1-cot x. Verify the identity. Explain each step please!

Answer 1

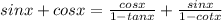`sinx+cosx=(cosx)/(1-tanx)+(sinx)/(1-cotx)\\` proved.

Explanation:

`sinx+cosx=(cosx)/(1-tanx)+(sinx)/(1-cotx)\\`

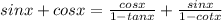
Taking R.H.S

`(cosx)/(1-tanx)+(sinx)/(1-cotx)\\`

Multiply and divide first term by cos x and second term by sinx

`=(cosx*cosx)/(cosx(1-tanx))+(sinx*sinx)/(sinx(1-cotx))`

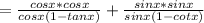
we know tanx = sinx/cosx and cotx = cosx/sinx

`=(cos^2x)/(cosx(1-(sinx)/(cosx) ))+(sin^2x)/(sinx(1-(cosx)/(sinx)))\\=(cos^2x)/(cosx-sinx)+(sin^2x)/(sinx-cosx)`

Taking minus(-) sign common from second term

`=(cos^2x)/(cosx-sinx)-(sin^2x)/(cosx-sinx)`

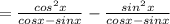
taking LCM of cosx-sinx and cosx-sinx is cosx-sinx

`=(cos^2x-sin^2x)/(cosx-sinx)`

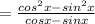
We know a^2-b^2 = (a+b)(a-b), Applying this formula:

`=((cosx+sinx)(cosx-sinx))/(cosx-sinx)\\=cosx+sinx\\=L.H.S`

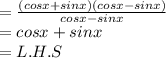
Hence proved