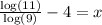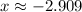Answer:
If you meant
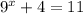 , then the answer is approximately 0.866.
, then the answer is approximately 0.866.
If you meant
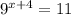 , then the answer is approximately -2.909 which looks like what you meant based on the choices.
, then the answer is approximately -2.909 which looks like what you meant based on the choices.
Explanation:
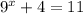
First step is to get the exponential part by itself. The part that has the variable exponent which is the
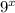 term.
term.
To do this we need to subtract 4 on both sides:
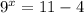
Simplify:
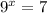
The equivalent logarithmic form is:

I always say to myself the logarithm is the exponent that is how I know what to put opposite the side containing the log.
Anyways if you don't have options for computing
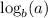 in your calculator you need to use the change of base formula.
in your calculator you need to use the change of base formula.

So
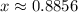
I don't see this as a choice so maybe you actually meant the following equation:
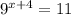
Let's see if this is the correct interpretation.
So the exponential part is already isolated.
So we just need to put in the equivalent logarithmic form:
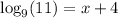
Now we subtract 4 on both sides:
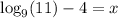
Again if you don't have the option for computing
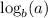 in your calculator, you will have to use the change of base formula:
in your calculator, you will have to use the change of base formula: