Question

The equation of a circle in general form is ​ x2+y2+20x+12y+15=0 ​ . What is the equation of the circle in standard form?

Answer 1

(x)²+(y)²=0

Explanation:

Answer 2

`{(x + 10)}^(2) + {(y + 6)}^(2) = 121`

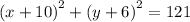
EXPLANATION

The equation of the circle in general form is given as:

`{x}^(2) + {y}^(2) + 20x + 12y + 15 = 0`

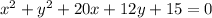
To obtain the standard form, we need to complete the squares.

We rearrange the terms to obtain:

`{x}^(2) + 20x + {y}^(2) + 12y = - 15`

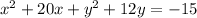
Add the square of half the coefficient of the linear terms to both sides to get:

`{x}^(2) + 20x +100 + {y}^(2) + 12y + 36 = - 15 + 100 + 36`

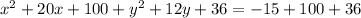
Factor the perfect square trinomial and simplify the RHS.

`{(x + 10)}^(2) + {(y + 6)}^(2) = 121`

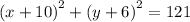
This is the equation of the circle in standard form.