Question

Game: roll two die. Win a prize based off the sum of the die rolled.

Cost of playing the game is $1
Prizes:
-Win $10 if your sum is odd.
-Win $5 if you roll a sum of 4 or 8.
-Win $50 if you roll a sum of 2 or 12.

Explain HOW to find the expected value of playing this game. What is the expected value of playing this game? Please show your work.

Interpret the meaning of the expected value in the context of this game. Why should someone play or not play this game? Please give your answer in complete sentences.

Answer 1

Let
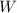`W` be the random variable representing the winnings you get for playing the game. Then

`W=\begin{cases}9&\text{if the sum is odd}\\4&\text{if the sum is 4 or 8}\\49&\text{if the sum is 2 or 12}\\-1&\text{otherwise}\end{cases}`

First thing to do is determine the probability of each of the above events. You roll two dice, which offers 6 * 6 = 36 possible outcomes. You find the probability of the above events by dividing the number of ways those events can occur by 36.

• The sum is odd if one die is even and the other is odd. This can happen 2 * 3 * 3 = 18 ways. (3 ways to roll even with the first die, 3 ways to roll odd for the die, then multiply by 2 to count odd/even rolls)
• The sum is 4 if you roll (1, 3), (2, 2), or (3, 1), and the sum is 8 if you roll (2, 6), (3, 5), (4, 4), (5, 3), or (6, 2). 8 ways.
• The sum is 2 if you roll (1, 1), and the sum is 12 if you roll (6, 6). 2 ways.
• There are 36 total possible rolls, from which you subtract the 18 that yield a sum that is odd and the other 10 listed above, leaving 8 ways to win nothing.

So the probability mass function for this game is

`P(W=w)=\begin{cases}\frac12&\text{for }w=9\\\frac29&\text{for }w=4\text{ or }w=-1\\\frac1{18}&\text{for }w=49\\0&\text{otherwise}\end{cases}`

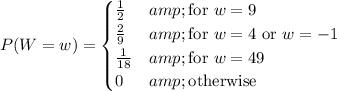
The expected value of playing the game is then

`E[W]=\displaystyle\sum_ww\,P(W=w)=\frac{71}9`

or about $7.89.

The expected value is positive, so a player can expect to earn money in the long run, and so should play the game.