Question

Expected Value (50 points)

Game: Roll two dice. Win a prize based on the sum of the dice.
Cost of playing the game: $1
Prizes:
Win $10 if your sum is odd.
Win $5 if you roll a sum of 4 or 8.
Win $50 if you roll a sum of 2 or 12.

Explain HOW to find the expected value of playing this game. What is the expected value of playing this game? Show your work. (30 points)

Someone want to help me find the expected value? I know how to do it with single things but not ones this complex.

Help is much appreciated

Answer 1

Let
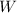`W` be the random variable representing the winnings you get for playing the game. Then

`W=\begin{cases}10-1=9&\text{if the dice sum is odd}\\5-1=4&\text{if the dice sum is 4 or 8}\\50-1=49&\text{if the dice sum is 2 or 12}\\-1&\text{otherwise}\end{cases}`

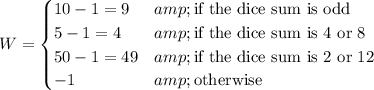
First thing to do is determine the probability of each of the above events. You roll two dice, which offers 6 * 6 = 36 possible outcomes. You find the probability of the above events by dividing the number of ways those events can occur by 36.

• The sum is odd if one die is even and the other is odd. This can happen 2 * 3 * 3 = 18 ways. (3 ways to roll even with the first die, 3 ways to roll odd for the die, then multiply by 2 to count odd/even rolls)
• The sum is 4 if you roll (1, 3), (2, 2), or (3, 1), and the sum is 8 if you roll (2, 6), (3, 5), (4, 4), (5, 3), or (6, 2). 8 ways.
• The sum is 2 if you roll (1, 1), and the sum is 12 if you roll (6, 6). 2 ways.
• There are 36 total possible rolls, from which you subtract the 18 that yield a sum that is odd and the other 10 listed above, leaving 8 ways to win nothing.

So the probability mass function for this game is

`P(W=w)=\begin{cases}\frac12&\text{for }w=9\\\frac29&\text{for }w=4\text{ or }w=-1\\\frac1{18}&\text{for }w=49\\0&\text{otherwise}\end{cases}`

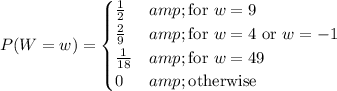
The expected value of playing the game is then

`E[W]=\displaystyle\sum_ww\,P(W=w)=\frac92+\frac89-\frac29+(49)/(18)=\frac{71}9`

or about $7.89.