Question

Which represents the solution of the system of equations, y=x^2-x+1 and y=x? Determine the solution set by graphing

Answer 1

(1,1)

Explanation:

We have the following system:

`y=x^2-x+1`

`y=x`

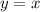
We are going to plug the 2nd equation into the 1st eqaution giving us:

`x=x^2-x+1`

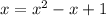
Now time to solve
`x=x^2-x+1`.

`x=x^2-x+1`

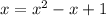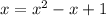
Subtract x on both sides:

`0=x^2-2x+1`

Now this actually not too bad. This a perfect square trinomial. That is it is of the form
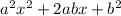`a^2x^2+2abx+b^2` which equals
`(ax+b)^2`.

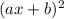So solving
`0=x^2-2x+1` is equivalent to solving
`0=(x-1)^2`

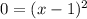
In order to solve
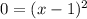`0=(x-1)^2`, we just need to know when x-1=0 which is at x=1. I got by adding 1 on both sides of x-1=0

Now remember y=x means we have the solution (1,1).

Okay, I'm going to leave all of this algebra here. I'm going to graph this without a graphing calculator.

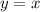`y=x` is a line with slope 1 and y-intercept 0.

`y=x^2-x+1` is a parabola. The vertex isn't obvious to me right now without the algebra but I do know the parabola is open up because the coefficient of x^2 being positive.

So let's find the vertex.

I'm going to start with the x-coordinate which is -b/(2a).

Compare
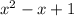`x^2-x+1` to
`ax^2+bx+c` and you should see that
`a=1,b=-1,c=1`.

So
`-(b)/(2a)=-(-1)/(2(1))=(1)/(2)`

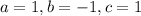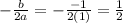
So the vertex occurs when the x-coordinate is 1/2.

To find the correspond y-value just use the equation that relations x and y.

That is use
`x^2-x+1`.

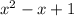Replace x with 1/2.

`((1)/(2))^2-((1)/(2))+1`

`(1)/(4)-(1)/(2)+1`

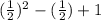
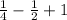
Find a common denominator.

`(1)/(4)-(2)/(4)+(4)/(4)`

`(1-2+4)/(4)`

`(3)/(4)`

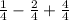
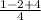
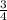
So the vertex is at (1/2,3/4) and the parabola is open up.

When you plug in 0 into
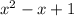`x^2-x+1` you get
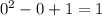`0^2-0+1=1` so the ordered pair (0,1) is on the parabola.

Using symmetry about the line x=1/2 we know that (1,1) is also on this graph.

Let's use this information to produce a graph now.

Now our answer appears to be (1,1) in the graph.

We can check this answer by plugging in (1,1) into our system and see if both equations check out:

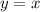`y=x` gives us 1=1 which is true. So we are good there.

`y=x^2-x+1` gives us
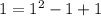`1=1^2-1+1` which is true. So we are good there.

The work for showing
`1=1^2-1+1`.

`1^2-1+1`

`1-1+1`

`0+1`

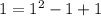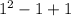
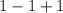
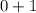
1

So the point (1,1) checks out for both of our equations which means it is a common point amongst the equations given.