Answer:
Q(-2,-7)
See attachment
Explanation:
We need to form a simultaneous equation and solve.
The point P has coordinates (1,8). Let the other point Q also have coordinate (x,y).
Then the average rate of change is the slope of the secant line connecting P(1,8) and Q(x,y) and this has a value of 5.
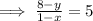
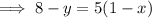

This point Q also lies on the given parabola whose equation is
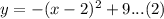
Put equation (1) into (2) to get:
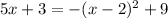
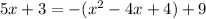
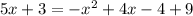
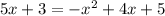
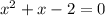
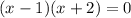
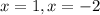
When x=-2, y=5(-2)-3=-7
Therefore the required point is Q(-2,-7)