Question

The drag force pushes opposite your motion as you ride a bicycle. If you double your speed, what happens to your force?

Answer 1

Answer: The drag force increases by a factor of 4

Explanation:

The Drag Force equation is:

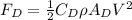`F_(D)=(1)/(2)C_(D)\rho A_(D)V^(2)` (1)

Where:

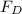`F_(D)` is the Drag Force

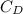`C_(D)` is the Drag coefficient, which depends on the material

`\rho` is the density of the fluid where the bicycle is moving (air in this case)

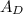`A_(D)` is the transversal area of the body or object

`V` the bicycle's velocity

Now, if we assume
`C_(D)`,
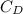`\rho` and
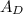`A_(D)` are constant (do not change) we can rewrite (1) as:

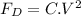`F_(D)=C.V^(2)` (2)

Where
`C` groups all these coefficients.

So, if we have a new velocity
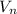`V_(n)` , which is the double of the former velocity:

`V_(n)=2V` (3)

Equation (2) is written as:

`F_(D)=C.(V_(n))^(2)=C.(2V)^(2)`

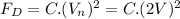
`F_(D)=4CV^(2)` (4)

Comparing (2) and (4) we can conclude the Drag force is four times greater when the speed is doubled.