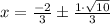Answer:

Explanation:
Compare
 to
to
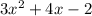 .
.
We have
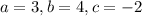 .
.
The quadratic formula is for solving equations of the form
 and is
and is
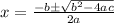 .
.
So we are going to plug in our values in that formula to find our solutions,x.
If you want to notice it in parts you can.
Example I might break it into these parts and then put it in:
Part 1: Evaluate
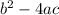
Part 2: Evaluate
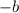
Part 3: Evaluate
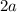
------Let's do these parts.
Part 1:
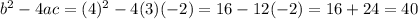 .
.
This part 1 is important in determining the kinds of solutions you have. It is called the discriminant. If it is positive, you have two real solutions. If it is negative, you have no real solutions (both of the solutions are complex). If it is 0, you have one real solution.
Part 2:
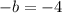 since
since
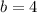 .
.
Part 3:
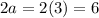 .
.
Let's plug this in:
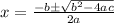
or in terms of our parts:

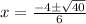
40 itself is not a perfect square but it does contain a factor that is. That factor is 4.
So we are going to rewrite 40 as
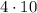 .
.
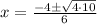
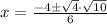
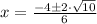
I'm going to go ahead and separate the fraction like so:
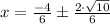
Now I'm going to reduce both fractions: