Question

Is 24/40=4/7 a true proportion? Justify your answer

Answer 1

A proportion

`a/ b = c/ d`

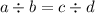
is nothing but a comparison between two fractions: we can rewrite it as

`(a)/(b)=(c)/(d)`

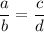
So, we can multiply both sides by the two denominators b and d to get

`(a)/(b)=(c)/(d) \iff ad = bc`

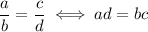
In other words, a proportion is true if the product of the inner terms is the same as the product of the outer terms.

In your case, we have the check is the following:

`24 / 40 = 4/ 7 \iff 24\cdot 7 = 40\cdot 7 \iff 168 = 280`

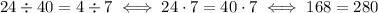
which is clearly false. So, 24:40 = 4:7 is not a true proportion. In fact, if we convert fractions into numbers, we have

`(24)/(40) = 0.6,\quad (4)/(7) = 0.\overline{571428}`

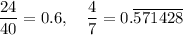
which makes even more clear that the proportion doesn't hold.