Question

Find the vertices and foci of the hyperbola with equation x^2/4 - y^2/60 = 1

Answer 1

Vertices of hyperbola: (2,0) and (-2,0)

Foci of hyperbola: (8,0) and (-8,0)

Explanation:

The given equation is:

`(x^2)/(4)-(y^2)/(60)=1`

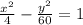
The standard form of equation of hyperbola is:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

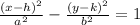
Center of hyperbola is (h,k)

Comparing given equation with standard equation

h=0, k=0

so, Center of hyperbola is (0,0)

Vertices of Hyperbola

Vertices of hyperbola can be found as:

The first vertex can be found by adding h to a

a^2 - 4 => a=2, h=0 and k=0

So, first vertex is (h+a,k) = (2,0)

The second vertex can be found by subtracting a from h

so, second vertex is ( h-a,k) = (-2,0)

Foci of Hyperbola

Foci of hyperbola can be found as

The first focus of hyperbola can be found by adding c to h

Finding c (distance from center to focus):

`c=√(a^2+b^2)  \\c=\sqrt{(2)^2+(2√(15))^2}\\c=8`

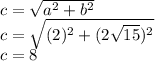
So, c=8 , h=0 and k=0

The first focus is (h+c,k) = (8,0)

The second focus is (h-c,k) = (-8,0)