Answer:
The solutions of the given equation are:
x=0,1,4 and 9
Explanation:
We are asked to find the solution of the equation:
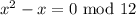
i.e. we have to find the possible values of x such that the equation is true.
then
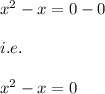
Hence, x=0 is the solution of the equation.
then
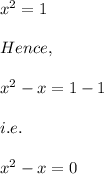
Hence, x=1 is a solution.
then
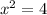
i.e.
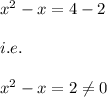
Hence, x=2 is not a solution.
then
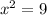
i.e.
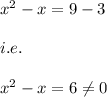
Hence, x=3 is not a solution.
then
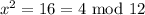
i.e.
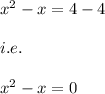
Hence, x=4 is a solution to the equation.
then
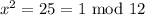
i.e.
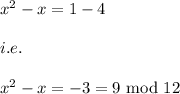
i.e.
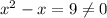
Hence, x=5 is not a solution.
then
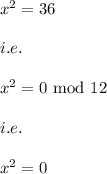
Hence,
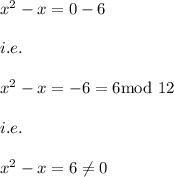
Hence, x=6 is not a solution
then,
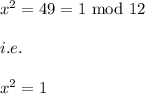
Hence,
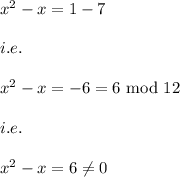
Hence, x=7 is not a solution.
then,
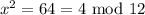
i.e.
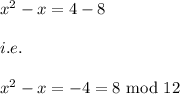
i.e.
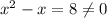
Hence, x=8 is not a solution.
then,
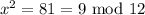
i.e.
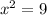
Hence,
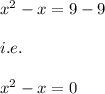
Hence, x=9 is a solution.
then,
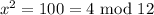
i.e.
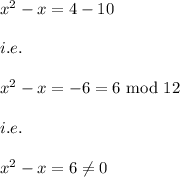
Hence, x=10 is not a solution.
then,
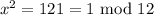
i.e.
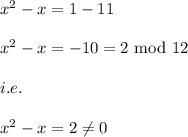
Hence, x=11 is not a solution.