Question

Suppose that 15% of people dont show up for a flight, and suppose that their decisions are independent. how many tickets can you sell for a plane with 144 seats and be 99% sure that not too many people will show up.

The book says to do this by using the normal distribution function and that the answer is selling 157 tickets.

Answer 1

Answer: 157 tickets

Explanation:

The people not showing up for the flight can be treated as from Binomial distribution.

The binomial distribution B(n, p) is approximately close to the normal i.e. N(np, np(1 − p)) for large 'n' and for 'p' and neither too close to 0 nor 1 .

Now, Let us assume 'n' = n

and we are given

p=0.15

So now B(n,0.15n) follows Normal distribution

u=n

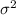`\sigma^(2)` = 0.15n

We have to calculate P(X<144) with 99% accuracy

P(X<144) = P(Z<z)

where;

z=
`(144-\bar{X})/ \sigma`

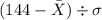
z score for 99% is 2.33

i.e.

`(144-\bar{X})/ \sigma = (144-n)/√(np) = 2.33\\\ (144-n)^(2) = \ np*2.33^(2)\\\ 20736 +n^(2) - 288n = 0.15n*5.43\\\ n^(2) - 288.81n + 20736=0`

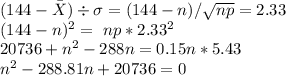
solving this we will get one root nearly equal to 157 and other root as 133

Hence the answer is 157.