Question

Identify the discontinuity and zero of the function f(x)= 4x/x^2-16

Answer 1

Explanation:

ANSWER

Point if discontinuity:

{x}= \pm3

Zero of the function is

x = 0

EXPLANATION

The given rational function is:

f(x) = \frac{3x}{ {x}^{2} - 9}

This function is not continous when

{x}^{2} - 9 = 0

{x}= \pm \sqrt{9}

{x}= \pm3

The function is zero when,

3x = 0

x = 0

Answer 2

x = 0 is the zero of this function and at x = ±4 function is discontinuous.

Explanation:

The given function is
`f(x) = (4x)/(x^(2)-16)`

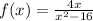
For this function we have to find the discontinuity and zeros of this function.

For zeros of the function
`0 = (4x)/(x^(2)-16)`

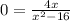
so zero of the function is x = 0

For x² - 16 = 0 this function not defined therefore, x = ± 4 function will be discontinuous.

Finally, x = 0 is the zero of this function and at x = ±4 function is discontinuous.