Question

Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. 2x-y=5 and 4x+ky=2

Answer 1

The system of linear equations has infinitely many solutions

Explanation:

Let's modified the equations and find the answer.

Using the first equation:

`2x-y=5` we can multiply by 2 in both sides, obtaining:

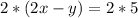`2*(2x-y)=2*5` which can by simplified as:

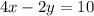`4x-2y=10` which is equal to:

`4x=2y+10`

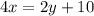
Considering the second equation:

`=4x+ky=2`

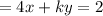
Taking into account that from the first equation we know that:
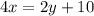`4x=2y+10`, we can express the second equation as:

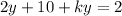`2y+10+ky=2`, which can be simplified as:

`(2+k)y=2-10`

`(2+k)y=-8`

`y=-8/(2+k)`

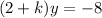
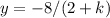
Because (-8) is being divided by (2+k), then (2+k) can't be equal to 0, so:

`2+k=0` if
`k=-2`

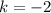
This means that k can be any number different than -2, and for each of these solutions, there is a different solution for y, allowing also, different solutions for x.

For example, if k=0 then

`y=-8/(2+0)` which give us y=-4, and, because:

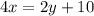`4x=2y+10` if y=-4 then
`x=(-8+10)/4=0.5`

Now let's try with k=-1, then:

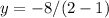`y=-8/(2-1)` which give us y=-8, and, because:

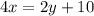`4x=2y+10` if y=-8 then
`x=(-16+10)/4=-1.5`.

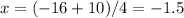Then, the system of linear equations has infinitely many solutions