Question

The smallest number which is divisible by both 306 and 657​

Answer 1

22,338 is the smallest number that is divisible by both 306 and 657. In other words, 22,338 is the least common multiple of 306 and 657.

Explanation:

The question is asking for the smallest number that is divisible by 306 and 657. That number in question is also known as the least common multiple of 306 and 657.

Neither 306 nor 657 is prime; the two numbers themselves are made of prime factors. For the number in question to be divisible by both 306 and 657, it needs to include the factors of both 306 and 657. However, for this number to be as small as possible, it needs to contain only the necessary factors and nothing else.

To find the factors required for this number, start by finding all the prime factors of the two divisors.

`\begin{aligned}306&=2 * 153\\ &= 2* 3 * 51\\ &= 2 * 3 * 3 * 17 \\ &= 2 * 3^(2) * 17\end{aligned}`.

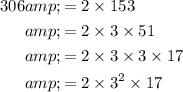In other words, the prime factors of 306 are:

• One
  `2`,
• Two
  `3`s, and
• One
  `17`.

Similarly,

`\begin{aligned}657&= 3 * 219\\ & = 3 * 3 * 73\\&=3^(2)* 73 \end{aligned}`.

The prime factors of 657 are:

• Two
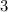  `3`s, and
• One
  `73`.

`\begin{array}l\text{Factor}& 306 & 657 & \text{New Number}\\\cline{1-4} \\[-1.0em]2 &\text{1 Occurrence}& \text{0 Occurrence} & \text{1 Occurrence}\\3 &\text{2 Occurrence} & \text{2 Occurrence}& \text{2 Occurrence}\\ 17 &\text{1 Occurrence}& \text{0 Occurrence} & \text{1 Occurrence}\\73 &\text{0 Occurrence}& \text{1 Occurrence} & \text{1 Occurrence}\end{array}`.

The number in question shall contain at least

• One
  `2`,
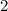• Two
  `3`,
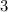• One
  `17`, and
• One
  `73`.

As a result, that number shall be equal to
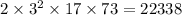`2 * 3^(2)* 17 * 73 = 22338`.