The vertices of the triangle are the points where any pair of lines intersect.
We start by setting up the system
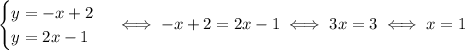
Using one of the two equations we can derive the correspondent y value:
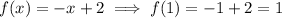
So, one vertex is (1, 1)
We choose the other two pairs of lines to find the other vertices:
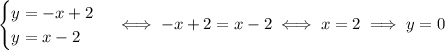
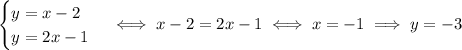
So, the three vertices are (1, 1), (2, 0), (-1, -3).