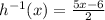Answer:
The inverse of h(x) is
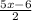
Explanation:
* Lets explain how to make the inverse of a function
- To find the inverse of a function we switch x and y and then solve
for new y
- You can make it with these steps
# write g(x) = y
# switch x and y
# solve for y
# write y as
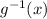
* Lets solve the problem
∵
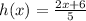
# Step 1
∴
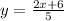
# Step 2
∴
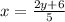
# Step 3
∵
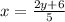
- Multiply each side by 5
∴ 5x = 2y + 6
- Subtract 6 from both sides
∴ 5x - 6 = 2y
- Divide both sides by 2
∴
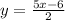
# Step 4
∴