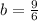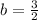Question

(x^2y^3) = (xy^a)^b

In the equation above, a and b are constants, and the
equation is true for all x > 0 and y > 0. What is the
value of a ?

The correct answer is C, 3/2

Thanks!

Answer 1

C.
`(3)/(2)`

Explanation:

To find the value f b, we need to compare the exponents.

The given exponential equation is:

`( {x}^(2) {y}^(3) )^(3) = ( {x} {y}^(a) )^(b)`

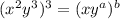
Recall and apply the following rule of exponents.

`( {x}^(m) )^(n) = {x}^(mn)`

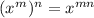
We apply this rule on both sides to get:

`{x}^(2 * 3) {y}^(3 * 3) = {x}^(b) {y}^(ab)`

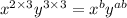
Simplify the exponents on the left.

`{x}^(6) {y}^(9) = {x}^(b) {y}^(ab)`

Comparing exponents of the same variables on both sides,

`b = 6 \: and \:\: ab = 9`

`\implies \: 6b = 9`

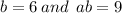
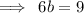
Divide both sides by 6.

`b = (9)/(6)`

`b = (3)/(2)`