Question

Determine if a triangle with side lengths 8, 14, and 15 is acute, right, or obtuse

Answer 1

Acute

Explanation:

The Converse of the Pythagorean Theorem states that:

• If
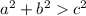  `a^2+b^2 > c^2` then the triangle is acute.
• If
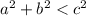  `a^2+b^2 < c^2` then the triangle is obtuse.
• If
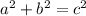  `a^2+b^2 = c^2` then the triangle is right.

The side lengths 8, 14, and 15 are given. We can assume the hypotenuse (or c) is the longest side length, so it is 15.

• c = 15

It doesn't matter which order of the numbers are plugged in for a and b, so a and b will be 8 and 14.

• a = 8
• b = 14

Now we have to add
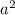`a^2` and
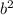`b^2` to see if the sum is greater than, less than, or equal to 15 (c).

• 
  `a^2 + b^2`
• 
  `8^2 + 14^2`

Calculate the rest of the problem.

• 
  `8^2=64 \\ewline 14^2=196`

• 
  `64+196=260`

We have to find what
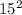`15^2` is before we can make a decision using the Converse of the Pythagorean Theorem.

• 
  `15^2=225`

260 (
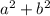`a^2+b^2`) is greater than 225 (
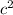`c^2`). This means that the triangle is acute because
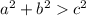`a^2+b^2>c^2`.