Answer:
4:9 ≠ 6:13
Explanation:
Given,
In triangle ABC,
D ∈ AB, E ∈ AC,
Also, AD = 4 unit, DB = 5 unit, AE = 6 unit, EC = 7 units,
Suppose,
DE ║ BC,
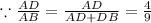

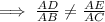
Because,
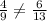
Which is a contradiction. ( if a line joining two points of two sides of a triangle is parallel to third sides then the resultant triangles have proportional corresponding sides )
Hence, DE is not parallel to segment BC.