Question

Cos y/ 1-sin y= 1+sin y/cos y. Verify the identity. Show All Steps!

Answer 1

When proving identities, the answer is in the explanation.

Explanation:

`(\cos(y))/(1-\sin(y))`

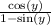
I have two terms in this denominator here.

I also know that
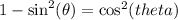`1-\sin^2(\theta)=\cos^2(theta)` by Pythagorean Identity.

So I don't know how comfortable you are with multiplying this denominator's conjugate on top and bottom here but that is exactly what I would do here. There will be other problems will you have to do this.

`(\cos(y))/(1-\sin(y)) \cdot (1+\sin(y))/(1+\sin(y))`

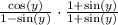
Big note here: When multiplying conjugates all you have to do is multiply fist and last. You do not need to do the whole foil. That is when you are multiplying something like
`(a-b)(a+b)`, the result is just
`a^2-b^2`.

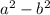Let's do that here with our problem in the denominator.

`(\cos(y))/(1-\sin(y)) \cdot (1+\sin(y))/(1+\sin(y))`

`(\cos(y)(1+\sin(y)))/((1-\sin(y))(1+\sin(y))`

`(\cos(y)(1+\sin(y)))/(1^2-\sin^2(y))`

`(\cos(y)(1+\sin(y)))/(1-\sin^2(y))`

`(\cos(y)(1+\sin(y)))/(cos^2(y))`

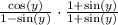
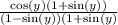
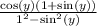
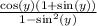
In that last step, I apply the Pythagorean Identity I mentioned way above.

Now You have a factor of cos(y) on top and bottom, so you can cancel them out. What we are really saying is that cos(y)/cos(y)=1.

`(1+\sin(y))/(cos(y))`

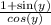
This is the desired result.

We are done.