Answer:
a=3
b=24
Explanation:
If
 is a factor of
is a factor of
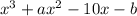 , then the factors of
, then the factors of
 must also be factors of
must also be factors of
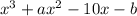 .
.
So what are the factors of
 ? Well the cool thing here is the coefficient of
? Well the cool thing here is the coefficient of
![x^2[tex] is 1 so all we have to look for are two numbers that multiply to be -12 and add to be positive 1 which in this case is 4 and -3.</p><p>-12=4(-3) while 1=4+(-3).</p><p></p><p>So the factored form of [tex]x^2+x-12]() is
is
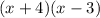 .
.
The zeros of
 are therefore x=-4 and x=3. We know those are zeros of
are therefore x=-4 and x=3. We know those are zeros of
 by the factor theorem.
by the factor theorem.
So x=-4 and x=3 are also zeros of
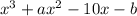 because we were told that
because we were told that
 was a factor of it.
was a factor of it.
This means that when we plug in -4, the result will be 0. It also means when we plug in 3, the result will be 0.
Let's do that.
 Equation 1.
Equation 1.
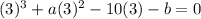 Equation 2.
Equation 2.
Let's simplify Equation 1 a little bit:

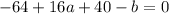
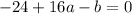
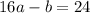
Let's simplify Equation 2 a little bit:
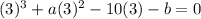
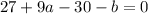

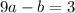
So we have a system of equations to solve:
16a-b=24
9a-b=3
---------- This is setup for elimination because the b's are the same. Let's subtract the equations.
16a-b=24
9a-b= 3
------------------Subtracting now!
7a =21
Divide both sides by 7:
a =3
Now use one the equations with a=3 to find b.
How about 9a-b=3 with a=3.
So plug in 3 for a.
9a-b=3
9(3)-b=3
27-b=3
Subtract 27 on both sides:
-b=-24
Multiply both sides by -1:
b=24
So a=3 and b=24