Answer:
Option A (134.7mm)
Explanation:
Let's find the distance, but first we need to remember that the distance between two points with coordinates (Xa,Ya) and (Xb,Yb) is defined by:
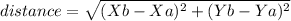
From the situation we notice that:
Xb=31.45 and Xa=65.35, as well as:
Yb=-55.50 and Ya=74.88
Using the previous equation we have:
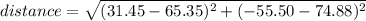
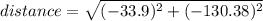
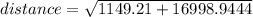
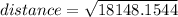
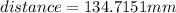
In conclusion, the distance between points (65.35,74.88) and (31.45,-55.50) is 134.7151mm, which is option A (134.7mm).