Answer:
A. 6.5
Explanation:
First we find the average
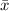 of the 9 data:
of the 9 data:
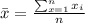
Where n is the data number, that in this case is 9.
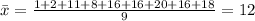
The formula of the standard deviation
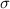 is:
is:
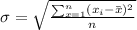
We replace the data and find the value of the standard deviation:
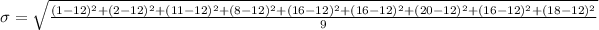
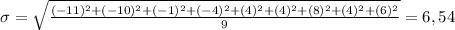
We approximate the number and the solution is 6,5