Answer:
If
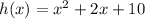 then
then
 .
.
If
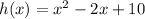 then
then
 .
.
Explanation:
In order to write the polynomial as the product of linear factors, we need to find the roots of the polynomial. A quadratic equation is defined as:

Because the given polynomial expression is a quadratic equation, we can use the following equations for calculating the roots:
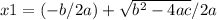

Since the second term sign is not given, then we can write the expression as:
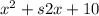 , in which a=1, b=s2 where 's' represents a sign (- or +), and c=10.
, in which a=1, b=s2 where 's' represents a sign (- or +), and c=10.
Using the equation for finding the roots we obtain:
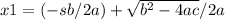
 ; notice that
; notice that

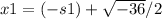
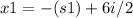
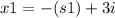
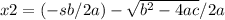
 ; notice that (s2)²=2^2
; notice that (s2)²=2^2

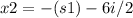
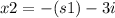
If we consider 's' as possitive (+) the roots are:
 and
and

Whereas if we consider 's' as negative (-) the roots are:
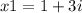 and
and
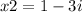
The above means that if the equation is
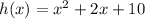 , then we can express the polynomial as:
, then we can express the polynomial as:
 .
.
But, if the equation is
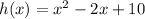 , then we can express the polynomial as:
, then we can express the polynomial as:
 .
.