Question

Solve 2cos theta+2=3 in the interval 0-2pi

Answer 1

`\theta=(\pi)/(3), (5\pi)/(3)`.

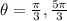Explanation:

`2\cos(\theta)+2=3`

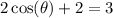
Subtract 2 on both sides:

`2\cos(\theta)=3-2`

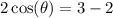
Simplify:

`2\cos(\theta)=1`

Divide both sides by 2:

`\cos(\theta)=(1)/(2)`

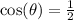
Now let's refer to the unit circle... When is the x-coordinate, 1/2?

There are 2 places this happens on [0,2pi].

One is in the first quadrant and the other in the fourth quadrant.

It is at
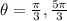`\theta=(\pi)/(3), (5\pi)/(3)`.