Question

A pig farmer owns a 20-arce farm and started business with 16 pigs. After one year, he has 421 pigs. Assuming a constant growth rate, how many pigs would he have after a total of 5.1 years?

Answer 1

The correct answer is 206550 pigs.

Explanation:

First of all you need to calculate the constant growth rate, which is given by the formula
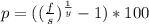`p=(((f)/(s) )^{(1)/(y) } -1)*100` where f is the value at the end of the year, s is the start value of that year, and y is the number of years.

From the excercise facts, we know that for 1 year (y=1), the final value is 421 (f=421), and the start value is 16 (s=16). Replacing them in the formula we get :
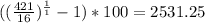`(((421)/(16)) ^{(1)/(1) } -1)*100 = 2531.25` So, the constant growth rate equals 2531.25.

Next, we have to multiply the starting amount of pigs times the constant growth rate times the amount of time that passed to get the final quantity of pigs. This would be
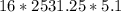`16*2531.25*5.1` and this gives us a total amount of 206550 pigs.

Have a nice day.