Answer:
1.99 pounds per gallon of salt in t=2 in the tank.
Explanation:
First we consider the matter balance equation that contemplates the input and output; the generation and consumption equal to the acomulation.
![Acomulation = Input - Output + Generation - Consumption]()
In this case we have no Generation neither do Consumption so, if we consider Acomulation = A(t), the rate of change of A(t) in time is given by:
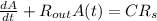 ---(1)
---(1)
where C is th concentration, with the initial value statement that A(t=0) = 0 because there is no salt in the time cero in the tank, only water.
Given the integral factor ->
![u(t)= exp[R_(out)]](https://img.qammunity.org/2020/formulas/mathematics/college/x4r4mblrwyqc1btt94414mmw0z0rct44us.png) and multipying the entire (1) by it, we have:
and multipying the entire (1) by it, we have:
![\int (d)/(dt)[A(t) \exp[R_(out)t]] \, dt = CR_(in) \int \exp[R_(out)t] \, dt](https://img.qammunity.org/2020/formulas/mathematics/college/qbmtig1fknkx8pfi9me8q9c6avj2rd5hdz.png)
Solving this integrals we obtain:
![A(t)=(CR_(in))/(R_(out))+Cte*\exp[-R_(out)t]](https://img.qammunity.org/2020/formulas/mathematics/college/lc9201w4xhol5w8lw0091yhejj9d1bxcxo.png)
So given the initial value condition A(t=0)=0 we have:
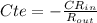 ,
,
and the solution is,
![A(t)=(CR_(in))/(R_(out))-(CR_(in))/(R_(out))\exp[-R_(out)t]](https://img.qammunity.org/2020/formulas/mathematics/college/swgppubjdfd8nh1et5t4amn8fmisoe8igw.png) .
.
If we give the actual values we obtain then,
![A(t)=2(pounds)/(gallon)-2(pounds)/(gallon) \exp[-3t]](https://img.qammunity.org/2020/formulas/mathematics/college/vpu97ri9n3rlpjixnoo0kl61n6bmbn2e0g.png) .
.
So in t= 2 we have
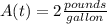 .
.