Question

What is the solution set of this system of equations?

y=x2-3x-4
x=y+8
A {(-1.0), (4.0)}
B. {(8.0). (0.8)}
c. {(0.0)}
D. {(2. -6)
E
There is no real solution.
Reset
Next

Answer 1

There is no real solutions


You can test each coordinate answer into each equation, and what ever coordinate pair cause both equations to be equal, then that would be the answer. But in this case, to the looks of it there is no solution for this.

Answer 2

No real solutions.

Explanation:

`y=x^2-3x-4`

`x=y+8`

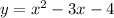
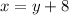
I'm going to subtract the second expression for y and plug it into the first equation.

So solving x=y+8 for y by subtracting 8 on both sides gives us y=x-8.

I'm going to insert this for the first y like so:

`x-8=x^2-3x-4`

Now I'm going to move everything to one side.

I'm going to subtract x on both sides and add 8 on both sides.

`0=x^2-3x-x-4+8`

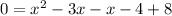
Simplifying:

`0=x^2-3x+4`

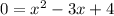
Now our job since the coefficient of x^2 is 1 is to find two numbers that multiply to be 4 and at the same time add up to be -3. I can't think of any such numbers.

Let's check the discriminant.

Compare
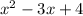`x^2-3x+4` to
`ax^2+bx+c`.

So
`a=1,b=-3,c=4`.

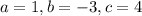The discriminant is
`b^2-4ac`.

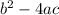So plugging in our numbers we get
`(-3)^2-4(1)(4)`.

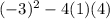Time to simplify:

`(-3)^2-4(1)(4)`

`9-16`

`-7`

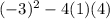
So since the discriminant is negative, then the solutions will not be real.