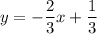Answer:
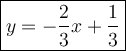
Explanation:
The slope-intercept form of an equation of a line:
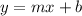
m - slope
The formula of a slope:
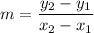
===============================================
We have the points (2, -1) and (5, -3). Substitute:
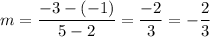
We have the equation:
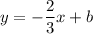
Put the coordinates of the point (2, -1):
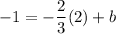
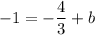 add 4/3 to both sides
add 4/3 to both sides
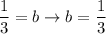
Finally: