Question

Let theta be an angle in quadrant II such that cos theta = -2/3

Find the exact values of csc theta and tan theta.

Answer 1

`tan\theta{3}=-(\sqrt5)/(2)`

`cosec\theta=(3)/(\sqrt5)`

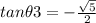
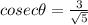
Explanation:

We are given that
`\theta` be an angle in quadrant II and
`cos\theta=-(2)/(3)`

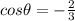
We have to find the exact values of
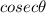`cosec\theta` and
`tan\theta`.

`sec\theta=(1)/(cos\theta)`

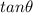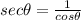
Then substitute the value of cos theta and we get

`sec\theta=(1)/(-(2)/(3))`

`sec\theta=-(3)/(2)`

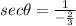
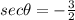
Now,
`1+tan^2\theta=sec^2\theta`

`tan^2\theta=sec^2\theta-1`

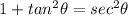
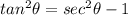
Substitute the value of sec theta then we get

`tan^2\theta= (-(3)/(2))^2-1`

`tan^2\theta=(9)/(4)-1=(9-4)/(4)=(5)/(4)`

`tan\theta=\sqrt{(5)/(4)}=-(\sqrt5)/(2)`

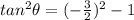
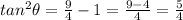
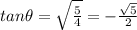
Because
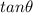`tan\theta` in quadrant II is negative.

`sin^2\theta=1-cos^2\theta`

`sin^2\theta=1-(\farc{-2}{3})^2`

`sin^2\theta=1-(4)/(9)`

`sin^2\theta=(9-4)/(9)=(5)/(9)`

`sin\theta=\sqrt{(5)/(9)}`

`sin\theta=(\sqrt5)/(3)`

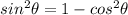
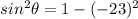
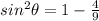
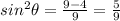
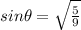
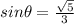
Because in quadrant II
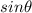`sin\theta` is positive.

`cosec\theta=(1)/(sin\theta)=(1)/((\sqrt5)/(3))`

`cosec\theta=(3)/(\sqrt5)`

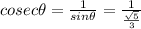
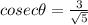
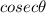`cosec\theta` is positive in II quadrant.

Answer 2

So we have
`\csc(\theta)=(3 √(5))/(5) \text{ and } \tan(\theta)=(-√(5))/(2)`.

Explanation:

Ok so we are in quadrant 2, that means sine is positive while cosine is negative.

We are given
`\cos(\theta)=(-2)/(3)(\frac{\text{adjacent}}{\text{hypotenuse}})`.

So to find the opposite we will just use the Pythagorean Theorem.

`a^2+b^2=c^2`

`(2)^2+b^2=(3)^2`

`4+b^2=9`

`b^2=5`

`b=√(5)` This is the opposite side.

Now to find
`\csc(\theta)` and
`\tan(\theta)`.

`\csc(\theta)=\frac{\text{hypotenuse}}{\text{opposite}}=(3)/(√(5))`.

Some teachers do not like the radical on bottom so we will rationalize the denominator by multiplying the numerator and denominator by sqrt(5).

So
`\csc(\theta)=(3)/(√(5)) \cdot (√(5))/(√(5))=(3 √(5))/(5)`.

And now
`\tan(\theta)=\frac{\text{opposite}}{\text{adjacent}}=(√(5))/(-2)=(-√(5))/(2)`.

So we have
`\csc(\theta)=(3 √(5))/(5) \text{ and } \tan(\theta)=(-√(5))/(2)`.