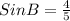Question

If in right triangle ABC with right angle C, sin A = 3/5 then what is the value of sin B?

Answer 1

Check the picture below.

Answer 2

For this case we have to define trigonometric relationships in rectangular triangles that the sine of an angle is given by the leg opposite the angle, on the hypotenuse of the triangle.

If we have to:

`Sin A = \frac {3} {5}`

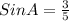
So:

Leg opposite angle A is: 3

The hypotenuse is: 5

If we apply the Pythagorean theorem, we find the value of the other leg:

`x = \sqrt {5 ^ 2-3 ^ 2}\\x = \sqrt {25-9}\\x = \sqrt {16}\\x = 4`

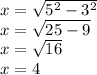
So, the Sine of B is given by:

`Sin B = \frac {4} {5}`

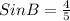
Answer:

`SinB = \frac {4} {5}`