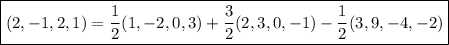Question

10. Determine whether or not, vectors ui(1,-2, 0, 3), u2 = (2, 3,0,-1), u3 = (3,9,-4,-2) e R is a linear combination of the (2,-1,2,1) 2

Answer 1

If (2, -1, 2, 1) is a linear combination of the three given vectors, then there should exist
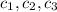`c_1,c_2,c_3` such that

`(2,-1,2,1)=c_1(1,-2,0,3)+c_2(2,3,0,-1)+c_3(3,9,-4,-2)`

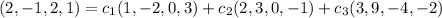
or equivalently, there should exist a solution to the system

`\begin{cases}c_1+2c_2+3c_3=2\\-2c_1+3c_2+9c_3=-1\\-4c_3=2\\3c_1-c_2-2c_3=1\end{cases}`

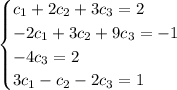
Right away we get
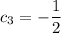`c_3=-\frac12`, so the system reduces to

`\begin{cases}c_1+2c_2=\frac72\\\\-2c_1+3c_2=\frac72\\\\3c_1-c_2=0\end{cases}`

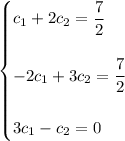
Notice that the first equation is the sum of the latter two. The third equation gives us

`3c_1-c_2=0\implies 3c_1=c_2`

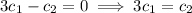
so that in the second equation,

`-2c_1+3c_2=\frac72\implies7c_1=\frac72\implies c_1=\frac12`

which in turn gives

`3c_1=c_2\implies c_2=\frac32`

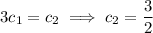
and hence the (2, -1, 2, 1) is a linear combination of the given vectors, with

`\boxed{(2,-1,2,1)=\frac12(1,-2,0,3)+\frac32(2,3,0,-1)-\frac12(3,9,-4,-2)}`