Derivative of f(x)=5.2x+2.3

Question

asked May 14, 2020 141k views

2 Answers

Cloudy · Answer 1 · 2020-05-19T07:34:09+0000

Answer:

5.2

Explanation:

Since you have a linear function, asking for derivative is equivalent to asking for the slope.

The slope of y=5.2x+2.3 is 5.2 so the derivative is 5.2 .

However, if you really want to use the definition of derivative, you may.

That is,
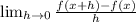$\lim_(h \rightarrow 0) (f(x+h)-f(x))/(h)$ .

We know
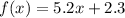f(x)=5.2x+2.3 so
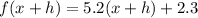f(x+h)=5.2(x+h)+2.3 . All I did was replace any x in the 5.2x+2.3 with (x+h) to obtain f(x+h).

Let's plug it into our definition:

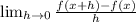
$\lim_(h \rightarrow 0) (f(x+h)-f(x))/(h)$

$\lim_(h \rightarrow 0) ([5.2(x+h)+2.3]-[5.2x+2.3])/(h)$

Now we need to do some distributing. I see I need this distributive property both for the 5.2(x+h) and the -[5.2x+2.3].

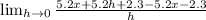
$\lim_(h \rightarrow 0) (5.2x+5.2h+2.3-5.2x-2.3)/(h)$

There are some like terms to combine in the numerator. The cool thing is they are opposites and when you add opposites you get 0.

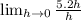
$\lim_(h \rightarrow 0) (5.2h)/(h)$

There is a common factor in the numerator and denominator. h/h=1.

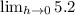
$\lim_(h \rightarrow 0)5.2$

5.2