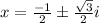Question

Given that (X+3) is a factor of the expression x^3 + 4x^2 + px + 3 , find the value of p. Hence, solve the equation x^3 + 4x^2 + px + 3=0, expressing the complex number in the form a + bi​

Answer 1

`p=4`

`x=(-1)/(2) \pm (√(3))/(2)i`

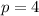
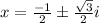
Explanation:

We are given (x+3) is a factor of
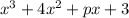`x^3+4x^2+px+3`, which means if were to plug in -3, the result is 0.

Let's write that down:

`(-3)^3+4(-3)^2+p(-3)+3=0`

`-27+36-3p+3=0`

`9-3p+3=0`

`9+3-3p=0`

`12-3p=0`

`12=3p`

`p=4`

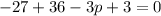
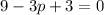
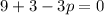
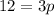
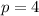
So the cubic equation is actually
`x^3+4x^2+4x+3=0` that they wish we solve for
`x`.

To find another factor of the given cubic expression on the left, I'm going to use synthetic division with that polynomial and (x+3) where (x+3) is divisor. Since (x+3) is the divisor, -3 will be on the outside like so:

-3 | 1 4 4 3

| -3 -3 -3

---------------------

1 1 1 0

So the other factor of
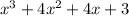`x^3+4x^2+4x+3` is
`(x^2+x+1)`.

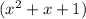We must solve
`x^2+x+1=0`.

Compare this to
`ax^2+bx+c=0`.

We have
`a=1,b=1, \text{ and } c=1`.

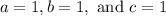The quadratic formula is

`x=(-b \pm √(b^2-4ac))/(2a)`.

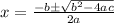Plug in the numbers we have for
`a,b, \text{ and } c`.

`x=(-1 \pm √(1^2-4(1)(1)))/(2(1))`.

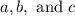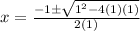Simplify inside the square root while also performing the one operation on bottom:

`x=(-1 \pm √(1-4))/(2)`

`x=(-1 \pm √(-3))/(2)`

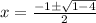
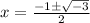
Now our answer will include an imaginary part because of that sqrt(negative number).

The imaginary unit is
`i=√(-1)`.

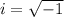So our final answer is:

`x=(-1)/(2) \pm (√(3))/(2)i`